Calculus is a foundational branch of mathematics‚ offering tools to analyze change and accumulation․ This introduction explores algebraic‚ numerical‚ and graphical methods‚ providing a comprehensive understanding of calculus concepts and their practical applications․
Importance of Calculus in Mathematics
Calculus is a cornerstone of modern mathematics‚ essential for understanding change‚ motion‚ and optimization․ It provides powerful tools for modeling real-world phenomena‚ from physics to economics․ By analyzing rates of change and accumulation‚ calculus solves complex problems that algebra alone cannot address․ Its principles underpin engineering‚ data analysis‚ and scientific research‚ making it indispensable․ The integration of algebraic‚ numerical‚ and graphical approaches allows for a holistic understanding‚ enabling versatile problem-solving․ This methodology bridges theoretical concepts with practical applications‚ fostering innovation across disciplines․ As a result‚ calculus remains a vital foundation for advancing mathematical and scientific knowledge․
Overview of Algebraic‚ Numerical‚ and Graphical Methods
Algebraic methods in calculus involve symbolic manipulation of equations and functions‚ providing exact solutions through algebraic techniques․ Numerical methods‚ on the other hand‚ rely on algorithms and approximations to solve problems that are difficult or impossible to solve algebraically; Graphical methods use visual representations‚ such as graphs of functions‚ to understand and analyze mathematical relationships․ Together‚ these approaches offer complementary perspectives‚ enabling a deeper understanding of calculus concepts․ Algebraic methods provide precision‚ numerical methods handle complexity‚ and graphical methods offer intuition․ Their integration allows for versatile problem-solving‚ making calculus accessible and applicable across various disciplines․ This combination is particularly emphasized in resources like the Finney‚ Demana‚ Waits‚ and Kennedy textbook‚ which blends these methodologies for comprehensive learning․
Algebraic Methods in Calculus
Algebraic methods in calculus involve solving equations and functions symbolically‚ providing precise solutions․ These techniques form the foundation of calculus problem-solving‚ as detailed in the Finney‚ Demana‚ Waits‚ and Kennedy textbook․
Definitions and Key Concepts
Calculus begins with fundamental definitions and concepts‚ including functions‚ graphs‚ and limits․ A function relates inputs to outputs‚ while its graph provides visual representation․ The concept of a limit defines the behavior of a function as it approaches a specific value․ Derivatives measure rates of change‚ and integrals calculate accumulation over intervals․ These ideas form the backbone of calculus‚ enabling the study of motion‚ optimization‚ and area․ Understanding these definitions is crucial for solving problems algebraically‚ as emphasized in the textbook by Finney‚ Demana‚ Waits‚ and Kennedy․ The interplay between algebraic‚ numerical‚ and graphical approaches relies heavily on these foundational concepts․
Solving Equations and Functions Algebraically
Algebraic methods in calculus involve solving equations and functions using symbolic manipulation․ Key concepts include variables‚ constants‚ and mathematical operations․ Solving equations often requires isolating variables to find their values․ For example‚ solving linear equations involves simplifying expressions‚ while quadratic equations may require factoring or using the quadratic formula․ Functions are central to calculus‚ and solving them algebraically involves evaluating them for specific inputs or finding their inverses․ Algebraic techniques also enable solving systems of equations and optimizing functions․ These methods are foundational for understanding derivatives and integrals․ The textbook by Finney‚ Demana‚ Waits‚ and Kennedy emphasizes balancing algebraic theory with practical problem-solving skills‚ ensuring students can apply these methods effectively in various calculus contexts․
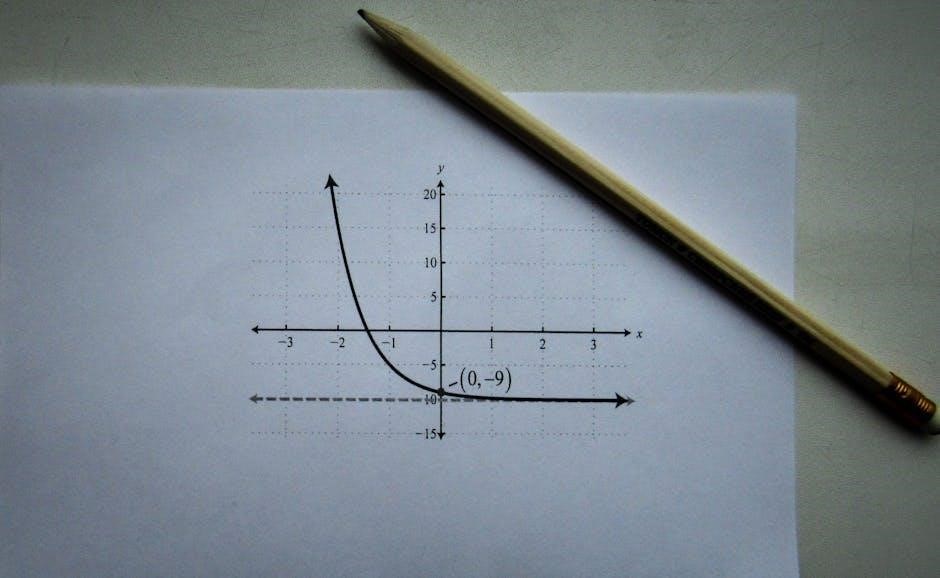
Numerical Methods in Calculus
Numerical methods provide approximate solutions to calculus problems when analytical solutions are complex or unavailable․ They rely on algorithms and iterative techniques‚ such as the Newton-Raphson method‚ to estimate derivatives and integrals․ These methods are particularly useful in real-world applications where precision is balanced with computational efficiency‚ as highlighted in resources like Finney‚ Demana‚ Waits‚ and Kennedy’s textbook․
Numerical solutions in calculus offer practical approaches to solve mathematical problems that cannot be easily addressed through algebraic methods․ These techniques rely on algorithms and iterative processes to approximate values‚ ensuring results are both accurate and computationally efficient․ Resources such as Finney‚ Demana‚ Waits‚ and Kennedy’s Calculus: Graphical‚ Numerical‚ Algebraic provide detailed explanations and examples of numerical methods․ By breaking down complex problems into manageable steps‚ numerical solutions enable students to explore realistic scenarios and understand the underlying principles of calculus․ This approach is particularly valuable in fields like engineering and physics‚ where precise calculations are essential․ The integration of numerical methods with graphical and algebraic techniques fosters a well-rounded understanding of mathematical concepts․
Approximation Techniques and Algorithms
Approximation techniques and algorithms are cornerstone tools in numerical calculus‚ enabling the estimation of solutions to complex mathematical problems․ Methods like the Newton-Raphson algorithm for root-finding and the Trapezoidal Rule for numerical integration provide systematic ways to approach equations that may not have straightforward algebraic solutions․ These techniques rely on iterative processes to refine approximations‚ ensuring a high degree of accuracy․ Resources such as Finney‚ Demana‚ Waits‚ and Kennedy’s Calculus: Graphical‚ Numerical‚ Algebraic offer in-depth guidance on implementing these methods․ By leveraging these algorithms‚ students can solve real-world problems efficiently‚ bridging the gap between theoretical calculus and practical applications in science‚ engineering‚ and other STEM fields․ These techniques underscore the versatility and power of numerical approaches in modern mathematics․

Graphical Methods in Calculus
Graphical methods in calculus involve analyzing functions through their visual representations‚ enabling intuitive understanding of derivatives and integrals․ These visual tools simplify complex concepts‚ aiding in problem-solving and real-world applications․

Understanding Graphs of Functions
Graphs of functions are essential in calculus for visualizing relationships between variables․ They provide insights into the behavior of functions‚ such as increasing or decreasing trends‚ maxima‚ minima‚ and points of inflection․ By analyzing graphs‚ students can identify key features like intercepts‚ asymptotes‚ and symmetry‚ which are crucial for solving problems․ For instance‚ graphical representations of exponential and logarithmic functions help in understanding their growth rates and inverses․ Parametric equations are also effectively explored through graphs‚ revealing motion and trajectories․ Additionally‚ graphs facilitate the study of limits‚ continuity‚ and differentiability‚ making abstract concepts more tangible․ This visual approach complements algebraic methods‚ offering a holistic understanding of calculus principles and their practical applications in real-world scenarios․
Visualizing Limits‚ Derivatives‚ and Integrals

Visualizing limits‚ derivatives‚ and integrals through graphs enhances understanding of these fundamental calculus concepts․ Limits can be observed by analyzing the behavior of functions as they approach specific values‚ often revealing continuity or discontinuity․ Derivatives‚ representing rates of change‚ are graphically illustrated by the slope of tangent lines to curves․ Integrals‚ which calculate area under curves‚ can be visualized using accumulation diagrams․ Graphical representations of these concepts bridge algebraic and numerical approaches‚ making abstract ideas more intuitive․ For example‚ parametric equations and motion along curves can be explored graphically‚ while exponential and logarithmic functions reveal their behavior through growth rates․ This visual approach simplifies complex calculations and provides a practical foundation for advanced problem-solving in calculus․
Integration of Algebraic‚ Numerical‚ and Graphical Approaches
Combining algebraic precision‚ numerical approximations‚ and graphical insights enhances problem-solving in calculus․ This integrated approach fosters a deeper understanding of complex mathematical concepts and their real-world applications․
Combining Methods for Comprehensive Problem Solving
Combining algebraic‚ numerical‚ and graphical approaches provides a robust framework for solving complex calculus problems․ Algebraic methods offer precise solutions‚ while numerical techniques handle cases where exact solutions are elusive․ Graphical representations‚ such as function plots‚ provide visual insights‚ making abstract concepts more tangible․ By integrating these methods‚ students and professionals can verify solutions from multiple perspectives‚ ensuring accuracy and fostering a deeper understanding of mathematical relationships․ This holistic approach is particularly valuable in real-world applications‚ where problems often require a combination of techniques to model and analyze effectively․ The synergy between these methodologies enhances problem-solving efficiency and adaptability‚ making it a cornerstone of modern calculus education and practice․
Real-World Applications of Integrated Methods
Integrated approaches in calculus are essential for tackling real-world challenges․ By combining algebraic precision‚ numerical approximations‚ and graphical interpretations‚ professionals can model and analyze complex systems in engineering‚ physics‚ economics‚ and computer science․ For instance‚ engineers use these methods to design structures‚ optimize processes‚ and simulate dynamic systems․ In economics‚ they analyze market trends and forecast behaviors․ Physicists apply them to study motion and energy transformations․ Computer scientists leverage these techniques for machine learning and algorithm optimization․ The synergy of these methodologies enables solving problems that would be difficult or impossible with a single approach‚ demonstrating the practical value of calculus in addressing real-world scenarios effectively and comprehensively․
Calculus: Graphical‚ Numerical‚ Algebraic (PDF Resources)
PDF versions of calculus textbooks by Finney‚ Demana‚ Waits‚ and Kennedy are available online‚ offering comprehensive resources for algebraic‚ numerical‚ and graphical approaches to calculus studies․
Overview of the Textbook by Finney‚ Demana‚ Waits‚ and Kennedy
The textbook Calculus: Graphical‚ Numerical‚ Algebraic by Finney‚ Demana‚ Waits‚ and Kennedy is a renowned resource for learning calculus․ It integrates algebraic‚ numerical‚ and graphical approaches to provide a comprehensive understanding of calculus concepts․ The book is available in multiple editions‚ including the 5th edition‚ and is widely used in academic settings․ It includes detailed explanations‚ practical examples‚ and exercises that help students master calculus fundamentals․ The textbook also emphasizes real-world applications‚ making it accessible and engaging for learners․ PDF versions of the book are available online‚ offering convenience for students and educators․ This resource is particularly valued for its balanced approach to teaching calculus through diverse methodologies․
Availability of PDF Versions and Online Resources
PDF versions of Calculus: Graphical‚ Numerical‚ Algebraic are accessible online‚ providing students and educators with convenient access to the textbook․ Platforms like Pearson Education offer downloadable PDFs‚ while other websites host free versions for educational purposes․ Online resources complement the textbook‚ offering interactive tools‚ practice problems‚ and video tutorials․ These resources enhance learning by allowing users to explore calculus concepts through multiple formats․ Availability varies‚ with some editions requiring purchase and others being freely accessible․ Ensuring access to these materials supports a flexible and effective learning experience for calculus students worldwide․
Calculus‚ through algebraic‚ numerical‚ and graphical approaches‚ provides a robust framework for understanding change and accumulation․ Its methodologies‚ supported by accessible PDF resources‚ empower learners globally․
Final Thoughts on the Importance of Diverse Methodologies in Calculus
The integration of algebraic‚ numerical‚ and graphical approaches in calculus provides a holistic understanding of mathematical concepts․ Each method complements the others‚ fostering a deeper appreciation of problem-solving strategies․ Algebraic techniques offer precision‚ while numerical methods allow for approximation and practical applications․ Graphical representations‚ meanwhile‚ provide visual insights‚ making complex ideas more accessible․ Together‚ these methodologies empower learners to tackle real-world challenges with versatility and confidence․ The availability of resources like Calculus: Graphical‚ Numerical‚ Algebraic in PDF formats ensures accessibility‚ enabling students to explore and master these diverse approaches effectively․ This balanced approach underscores the value of a multifaceted education in calculus․